|
Some of you maybe know that, using a compass and unmarked straightedge, it's impossible to trisect any given angle. However, there are a number of ways to trisect any given angle using a particular tool or object.
One such object is a carpenter's square. A modern carpenter's square isn't really a square in the geometric sense, but is rather a metal L with one arm that's a little wider than the other. Carpenters use it for many different tasks in building a house, and ultimately it contributes to the house being "square" - meaning things are all at the correct angles.
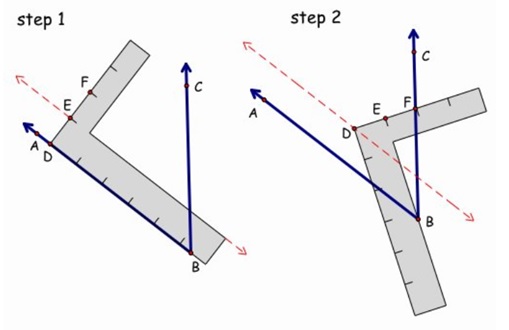
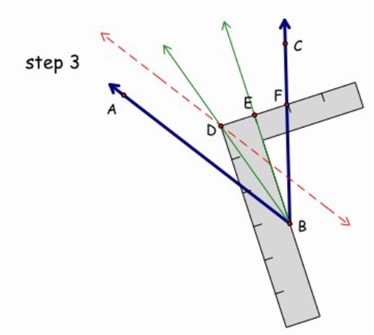
In the picture below, we're trying to trisect angle ABC. DE is equal to the width of the wide arm and so is EF.
Use the wide arm of the square to draw a line parallel to AB.
Lay the square so that the inside edge of the wide arm goes through B and the outer corner, D, lies on the new line, and F lies on CB.
Draw rays BD and BE.
Are rays BD and BE really trisectors of angle ABC?
|












